Previous - Number Theory

Converting Units

Polygon

A polygon is a plane shape (two-dimensional) with straight sides. Examples include triangles, quadrilaterals, pentagons and hexagons.

A regular polygon has:

• all sides equal and
• all angles equal

Quadrilaterals

A quadrilateral is a closed figure made up of four straight edges and four corners.

Types of Quadrilaterals:

The special types of quadrilaterals are listed below:

1. Parallelogram - A two-dimensional flat shaped closed figure made up of four sides where both pairs of opposite sides are parallel with same length is termed as parallelogram.
2. Rectangle - A two-dimensional flat shaped four sided closed figure made up of four sides and four right angles.
3. Rhombus - A two-dimensional flat shaped closed figure made up of four congruent sides.
4. Square - A two-dimensional flat shaped four sided closed figure made up of four equal sides and four right angles.
5. Trapezoid - A two-dimensional flat shaped four sided closed figure with at least one pair of parallel sides and each angle measures lesser than 180 ° .
6. Kite - A two-dimensional flat shaped closed figure made up of four sides such that each pair of consecutive sides is congruent.

Area

Area is a measure of how much space there is on a flat surface.

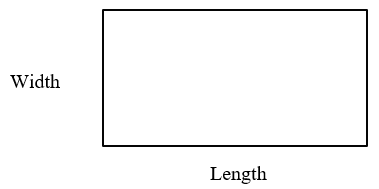
Rectangle

A rectangle is a four-sided shape whose corners are all ninety degree angles.  In a rectangle, two of the sides are equal (length) and the two other sides are equal (width).

The area of a rectangle is its length multiply by its width

"$A = Length \times Width$"

Example

Find the area of a rectangle with length of 8cm and width of 6 cm.

"$Area = 8 \times 6 = 48cm^2$"

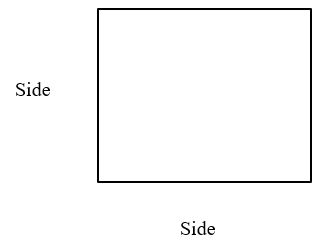
Square

A square is a flat shape defined by four points at the four corners. A square has four sides all of equal length, and four corners, all right angles (90 degree angles). All the sides of a square are equal.

"$ \text{The area of a square} = side \times side$"

Example

Find the area of a square with side of 7cm

"$Area = 7 \times 7 = 49cm^2$"

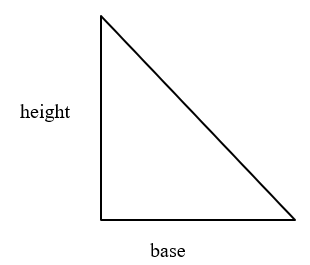
Triangle

A triangle is a polygon with three edges and three vertices.  A polygon is a plane shape with straight sides.

The area of a triangle = ½ base times height,

Example:

Find the area of a  triangle with height of 10 cm and base of 6 cm.

"$Area = \frac{1}{2} \times 6  \times 10 = 30cm^2$"

Heron's Formula

You can calculate the area of a triangle if you know the lengths of all three sides using a formula  called the Heron's Formula. 

This can be done as follows:

Step 1: Calculate "s" (half of the triangles perimeter):

"$s = \frac {a+b+c}{2}$"

Step 2: Then calculate the Area:

"$A =\sqrt {s(s-a) \times (s-b) \times (s-c)}$"

Example:

Find the area of a triangle with side of 8.

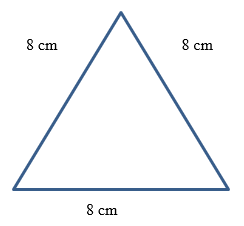
"$S = \frac {(8+8+8)}{2} = 12$"

"$A = \sqrt {12(12-8)\times(12-8)\times(12-8)}$"

"$  = \sqrt {12 \times 4 \times 4 \times 4}$"

"$  = \sqrt {768}$"

"$  = 27.71$"

Parallelogram

A parallelogram is a quadrilateral with two pairs of parallel sides.

The area of a parallelogram, "$A = bh$"

where, b is the length of the base of the parallelogram and h is the perpendicular height of the parallelogram.

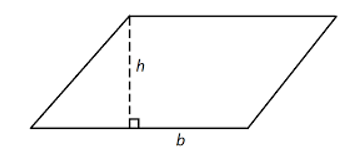
Example

Find the area of a parallelogram with base of 9cm and height of 5cm.

"$A = bh$"

"$= 9 \times 5 = 45cm^2$"

Trapezium

A trapezium is a quadrilateral with only one pair of parallel sides.

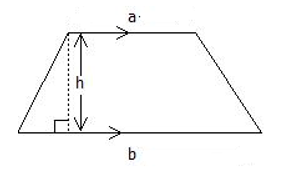
"$ \text{The area of a trapezium} = 1/2 (a + b) h $"

where, a is the length of one parallel side of the trapezium and b is the length of the second parallel side of the trapezium.

Kite

The area of a kite is given by the following formula where x and y are the lengths of the kite's diagonals:

"$A = 1/ 2 xy$"

where

"$AC = x$"

"$BD = y$"

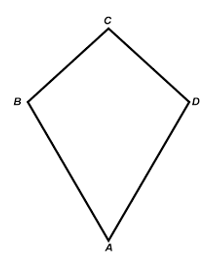
Example

Find the area of a kite where:

"$AC = 24cm$"

and

"$BD = 16 cm$"

Solution

"$1/2 \cdot (24 \cdot 16)  = 384 / 2 = 192cm^2$"

Rhombus

A rhombus is a four-sided shape where all sides have equal length. Also opposite sides are parallel and opposite angles are equal.  It is a quadrilateral all of whose sides have the same length.  A rhombus is actually just a special type of parallelogram. Many of the area calculations can be applied to them also. Choose a formula based on the values you know to begin with.

1. The "base times height" method

   First pick one side to be the base. Any one will do, they are all the same length. Then determine the altitude - the perpendicular distance from the chosen base to the opposite side. The area is the product of these two, or, as a formula:

   "$Area = b \times a$"

   where
   b is the length of the base
   a is the altitude (height).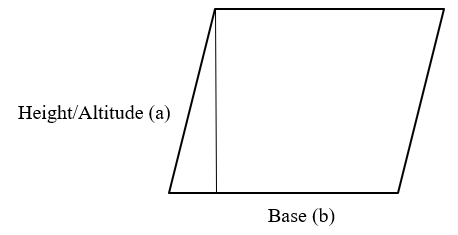

    

2. The "diagonals" method

   Another simple formula for the area of a rhombus when you know the lengths of the diagonals. The area is half the product of the diagonals. As a formula:

   "$Area = \frac {1}{2} d_1 d_2 $"

   where
   "$d_1$" is the length of a diagonal
   "$d_2$" is the length of the of the other diagonal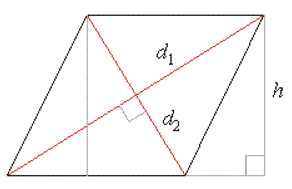

    

Example

Find the area of a rhombus with d₁ being 8cm and d₂ being 9 cm.

Solution

"$Area = \frac {1}{2} d_1 d_2 $"

"$ = (8 x 9)/2 = 72/2 = 36 cm^2$"

Circle

The area of a circle, "$A = \pi r^2$"

where, r is the radius of the circle

and, "$ \pi $" is "$3.142$" or "$22/7$"

Example

Find the area of a circle with radius of 14cm.

"$Area = 22/ 7 \times 14 \times 14 = 616cm^2$"

Perimeter

Perimeter deals with the total distance around an object such as square or rectangle.

Rectangle

The perimeter of a rectangle, "$P = L + w + L + w$"
                                                     "$= 2(L + w)$"

where, L is the length of the rectangle and w is the width of the rectangle.

Square

"$Perimeter = s + s + s + s$"

Triangle

The perimeter of a triangle, P = the sum of all the sides.

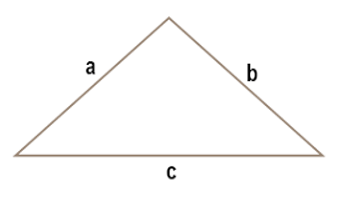
"$Perimeter = a + b + c$"

Circle

The perimeter of a circle is called its circumference. The circumference of a circle, "$C = 2 \pi r$" or πd where, r is the radius of the circle and d is the diameter of the circle with "$ \pi $" being "$22/7$" or "$3.142$".

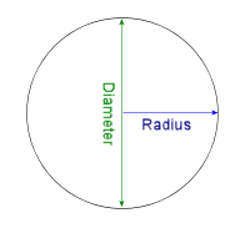
Example

Find the perimeter of a square with radius of 7cm. 

Solution

"$Perimeter, P = 2 \times 22/ 7 \times 7$"

= 44cm.

Area of a Sector and Arc Length

The sector of a circle is the portion enclosed by two radii and an arc. The smaller area is called the minor sector and the larger area, the major sector.

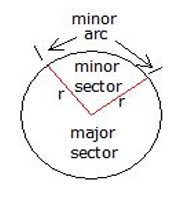
The arc length of the minor sector (minor arc), is the portion of the circumference of the circle which spans the minor sector.

The area of the sector of a circle, "$A = \pi r^2 \frac {\theta}{360}$"

The length of the arc, "$L = 2 \pi r = \pi r \frac {\theta}{360}$"

The perimeter of a sector "$= 2r + 2 r \pi (\theta/180^0 )$".

Example:

1. ) Calculate the length of the major arc x y z
2. ) Evaluate the area of the major sector x y z

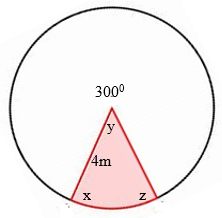
Solution:

1. )"$ \text{The length of the major arc x y z} = 2 \pi r = \pi r^2 \frac{\theta}{360} $"
   "$= 2 (3.142) \times 4 \times 0.83 $"
   "$= 20.86m$"
2. )"$ \text{The area of the sector of a circle, A} = \pi r^2 \frac{\theta}{360}$"
   "$= 3.142 \times 4 \times 4 \times 0.83$"
   "$= 41.73m^2$"

Example:

The minute hand on the clock is 50 cm long. What area does it pass over in 30 minutes?

Solution:

"$ \text{Area of the sector of a circle} = \pi r^2 \frac{\theta}{360}$"

"$= 3.142 \times 50 \times 50 \times 30/60$"
"$= 3.142 \times 50 \times 50 \times 0.50$"
"$= 3928cm^2$"

Example:

Calculate the radius of the sector shown below.

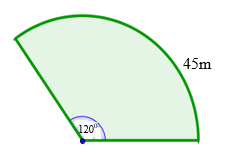
Solution:

The perimeter of circle "$= 2 \pi r$"

Because the angle of the circle is "$120^0$" which is "$1/3$" of the circle, we multiply the "$45$" by three to get the circumference of the entire circle which is:

"$ \text{Perimeter of the circle} = 45 + 45 +45$"
"$45 + 45 + 45 = 2 (3.142) r$"
"$135 = 6.284 r$"
"$r = 135/6.284 $"
"$r = 21.5$"

Example:

Calculate the perimeter of the following:

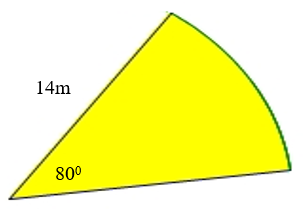
Solution:

"$ \text{The perimeter of a sector} = 2r + (2 \pi rx (\theta /180^0)$"
"$= 2 (14) + 2 \times 14 \times 3.142 \times 80/360$"
"$= 28 + 28 \times 3.142 \times 0.22$"
"$= 28 +19.4$"
"$= 47.1 m$"

Example:

Calculate the perimeter of the following:

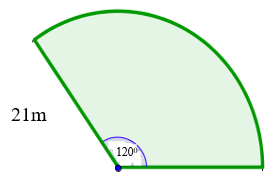
Solution:

"$ \text{The perimeter of a sector} = 2r + (\theta/180^0 \times 2 \pi r)$"
"$= 2 (21) + 2 \times 21 \times 3.142 \times 0.33$"
"$= 42 + 2 \times 21 \times 3.142 \times 0.33$"
"$= 42 + 43.55$"
"$= 85.55m$"

Next - Measurement 2: Surface Area and Volume