Previous - Measurement 1: Area and Perimeter
Surface Area
The surface area of a figure is the total area of all the sides of the figure.
Triangular Prism (Right Angle Triangle)

To find the surface area of the prism above, follow the steps below:
Divide the figure into smaller shapes, find the area of each smaller shape and then sum the areas of each smaller shape. A right-angle triangle prisim can be divided into five smaller shapes which are two right angle triangles and three rectangles.
Example
Find the surface area of the prism below.
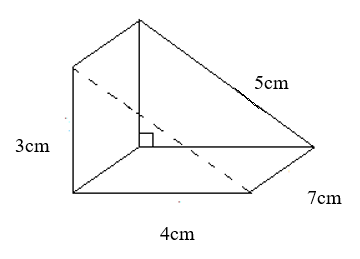
Area of right angle triangle = 1/ 2 base x height = 1/ 2 x 4 x 3 = 6
As there are 2 of these right angle triangles, we have 6 x 2 = 12
Area of rectangle 1: 4 x 7= 28
Area of rectangle 2: 5 x 7= 35
Area of rectangle 3: 3 x 7= 21
Surface area = 12 + 28 + 35 + 21 = 96cm2
Pyramid
A pyramid is a solid formed by connecting a polygonal base and a point, called the apex.
The surface area of a pyramid = Area of the base + 1/ 2 Perimeter of Base x Length of Side
Example
Find the surface area of the following pyramid
Surface area of pyramid = Area of base + 1/ 2 perimeter of base x length
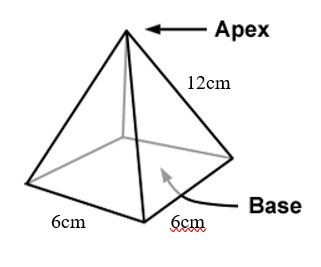
Area of 6 x 6 = 36cm2
Perimeter = 1/ 2 4(6) = 12cm
Surface area = 36 + 12 x 12 = 36 + 144 = 180 cm2
Cylinder

A cylinder can be divided into three parts: two circles and a curved surface area.
So the surface area = 2πr2 + 2πrh
The first term is the area of the two circles and the second term is the perimeter of the cylinder.
Example
Find the surface area of a cylinder with a radius of 3 cm, and a height of 2 cm.
Solution
SA = 2 × π × r2 + 2 × π × r × h
SA = 2 × 3.14 × 32 + 2 × 3.14 × 3 × 2
SA = 6.28 × 9 + 6.28 × 3 x 2
SA = 56.52 + 37.68
Surface area = 94.2 cm2
Cube
A cube has 6 sides or faces of the same surface area. Therefore, if the area of a square is side times side, then the surface area is S times S times 6.
Cuboid
A cuboid is an object with six flat faces and all angles are right angles with all its faces being rectangles.
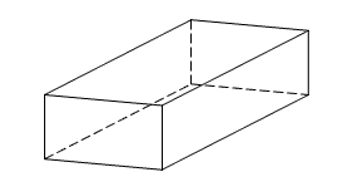
The surface area of a cuboid, A = 2Lw + 2 Lh + 2wh
where,
L is the length of the cuboid
w is the width and
h is the height of the cuboid.
Example
Find the surface area of a cuboid with length of 5cm, width 6cm and height 7cm.
Solution
A = 2Lw + 2 Lh + 2wh
= 2 x 5 x 6 + 2 x 5 x 7 + 2 x 6 x 7
= 60 + 70 + 84
= 214cm2
Sphere
A sphere is a three-dimensional object such as a ball or the globe with every point on the surface halfway from the center.
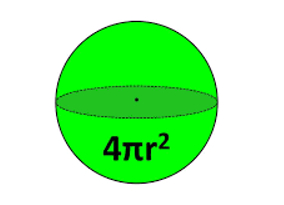
The surface area of a sphere, A = 4πr2
where, r is the radius of the sphere.
Example
Find the surface area of a sphere with radius of 9cm.
Solution
Surface Area of a sphere, A = 4 πr2
4 x 3.14 x 9 x 9 = 1018 cm2
Volume
Volume is the amount of 3-dimensional space an object occupies.
Cube
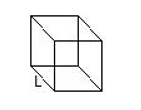
The volume of a cube , V = L3
where, L is the length of a side of the cube.
Example
The volume of a cube with side of 4cm = 4 x 4 x 4 = 64cm3
Cuboid
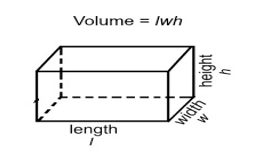
The volume of a cuboid, V = Lwh
where, L is the length of the cuboid,
w is the width and h is the height of the cuboid.
Sphere
The volume of a sphere, V = 4/3 πr3
where, r is the radius of the sphere.
Example
The volume of a sphere with radius of 7cm = 4/ 3 x 22/ 7 x 7 x 7 x 7 = 4/ 3 (22/ 7) 7x7x7 = 1436.9cm3
Triangular Prism (Right Angle Triangle)

The volume of a triangular prism, V = Area of one of the triangles times length
= 1/ 2 base x height x length of the triangular prism
Example
Find the volume of a triangular prism with base of 6cm, length of 8cm and height of 7cm.
Solution
Volume = 1/ 2 (6) x 7 x 8
= 3 x 7 x 8 = 168cm3
Pyramid
The volume of a pyramid = 1/ 3 Area x height.
Example
Find the volume of a pyramid with length of 9cm and height of 14cm.
Solution
V = 1/ 3 (9 x 9) x 14 =
= 27 x 14 = 378cm3
Cylinder
The volume of a cylinder, V = πr2h
where, πr2 is the area of the circular cross-section and h is the height of the cylinder.
Example
Find the volume of a cylinder with radius of 7 cm and height of 14cm.
Solution
Volume = 22/ 7 x 7 x 7 x 14
= 154 x 14 = 2155cm3
Distance, Speed and Time
There are mathematical problems that require students to be able to calculate distance, time and speed.
Distance = Speed x Time
Time = Distance/Speed
Speed = Distance/Time
Distance
Example
Joe drove from his home to the mall at an average speed of 50 kilometres an hour and took 4 hours to do so. Calculate the distance from his home to the mall.
Solution
Distance = Speed x Time = 50 x 4 = 200 kilometres.
Speed
Example
Sherry walked to the park located 80 kilometers in 5 hours. Calculate her speed per hour.
Speed = Distance/Time = 80/5 = 16 kilometers per hour.
Time
A lady travelled a distance of 45 kilometers at a speed of 5 kilometers per hour. Calculate the time she took.
Speed = Distance/ Speed = 45/5 = 9 hours