Previous - Geometry 1: Types and Properties of Angles and Triangles

Trigonometry, which studies the measure of triangles, takes algebra to the next level. Its most well-known features include the Pythagorean Theorem and the sine, cosine, and tangent ratios.

Pythagoras’ Theorem

Pythagoras’ theorem states that for a right angled triangle, if a square was to be drawn on each side of the triangle, the area of the square on the hypotenuse side (the side opposite the 90° angle), is equal to the sum of the area of the two squares drawn on the other two sides where, a, b and c are the sides of the triangle.

Pythagoras’ Theorem is most often employed to find the length of an unknown side of a triangle, and as such the form:

a² + b² = c²

Example:

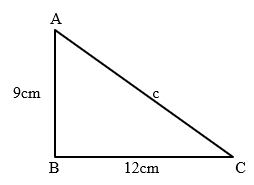
Find the length of side c cm.

9cm² + 12cm² = c²

81cm² + 144cm² = 225cm²

c² = 225cm²

c   = √225  = 15cm

Trigonometry - Sides of a Right Angled Triangle

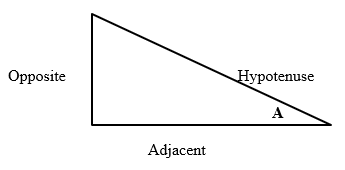
The order in which the names of the sides are determined is listed below:

• The longest side of the triangle is called the Hypotenuse.
• The side opposite to the angle under consideration, in this case A, is called the Opposite.
• The remaining side is called the Adjacent.

Note: the Opposite side is always the side opposite to the angle under consideration.

The three functions are:

Sine

ABC is a right angled triangle

a    is the symbol for the side opposite angle A

b    is the symbol for the side opposite angle B

c    is the symbol for the side opposite angle C

Example

Given the knowns, we need to find the unknown. The knowns are: hypotenuse = 7 and opposite = 3.5.  Therefore, we will need to find sine which is opposite/hypotenuse.

Solution

Sin (x) = Opposite / Hypotenuse = 3.5 / 7 = 0.5.  Therefore, the unknown which is the Adjacent which is the length of C is 0.5.

Having now known the length of C, we can now find the respective angle.  We can obtain this by solving for this equation which is:

sin(x) = 0.5

Next we can re-arrange that into this:

x = sin^-1 (0.5)

On the calculator, just key in 0.5 and use the sin^-1 button to get the answer:

x = 30°

The difference between sine and sine^-1 which is the inverse of sine is that sine gives the ratio of opposite/hypotenuse while sine^-1 gives us the angle.  

• Sine Function: sin(30°) = 0.5
• Inverse Sine Function: sin^-1(0.5) = 30°

Tangent

The ratio called tangent (tan) of an acute angle in a right angled triangle is defined as the ratio between the side opposite the angle and the side adjacent to the angle.

ABC is a right angled triangle

Tan A = a/b

Tan B = b/a

Example

Find the angle A

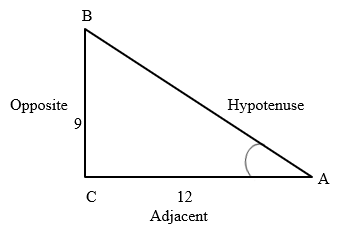
Solution

Tan A= a/b = 9/12 =  ¾ = 0.75

We need to use the inverse function for tan, tan^-1, to find the angle. This can be obtained by punching 0.75 on your calculator and using the inverse of tan to get:

tan^-1 = 37º

Example

If we have a = 4 and angle A = 37º 

Find the side of b.

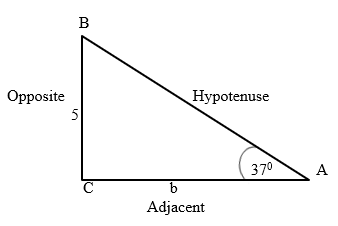
tan 37º = 5/b

tan 37º · b = 5

0.75· b = 5

b=6.7

Cosine

The cosine (cos) of an acute angle in a right angled triangle is the ratio between the side adjacent to the angle and the hypotenuse of the triangle.

ABC is a right angled triangle

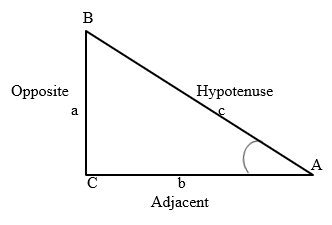
Cos A = b/c

Cos B = a/c

Example: Use the cosine function to find the angle A giving your answer to the nearest degree.

cos A = 3/5 = 0.6 gives <A= 53º

Shift cos-1 0.6 = 53º

Example: Find the side b.

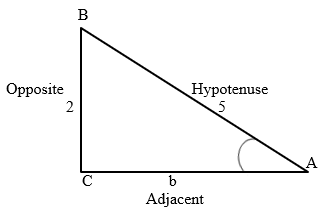
cos 53º = ^b/₅

b = Cos 53º · 5

b = 0.6 x 5.

b = 3.

Next - Geometry 3: Coordinate Geometry