Previous - Functions and Relations

BODMAS

BODMAS is the acronym to indicate the order in which arithmetic operations are carried out.

B – brackets, O – of (or times) M – multiplication, D – division, A – addition and S – subtraction of quantities in that order.

Whole Numbers

We will now be showing how to compute the addition, subtraction, multiplication and division of whole numbers.

Addition

Add the numbers 1543 and 724.

"$ \bbox[5px,border:2px solid black] { \begin{align} &&1543 & \\ & + \\ &&724 & \\ &&\overline{2267} & \end{align} } $"

Procedure: In addition, we add from right to left. The numbers in that column are 3 and 4 and when we add these, we will get 7. We then add 4 and 2 to get 6 then 7 and 5 to get 12. The 2 from the 12 is taken with the remainder of 1 to add to the existing 1 to get 2. So the answer from this addition is 2267.

Subtraction

Subtract 234 from 876.

"$ \bbox[5px,border:2px solid black] { \begin{align} &&&876 \\ & - \\ &&&\frac{234}{642} \end{align} } $"

Multiplication

Multiply 345 by 123.

"$ \bbox[5px,border:2px solid black] { \begin{align} &&345 & \leftarrow \text{Multiplicand} \\ & \times \\  &&123 & \leftarrow \text{Multiplier} \\ &&\overline{34500} & \\ &&6900 & \\  &&1035 & \\ &&\overline{42435} & \end{align} } $"

Procedure: When multiplying, multiply the top number or the Multiplicand (in this case 345) by each of the digits in the bottom number or the Multiplier (in this case 123), starting with the number to the left which is 1. On multiplying the top numbers by 1, we get a result of 345. This result is written with the 5 being exactly below the 1. Next, 345 is multiplied by the second digit of the multiplier which is 2 to obtain the result 690 with the 0 being placed directly below the number it is multiplied by which is 2. Next, the 345 is multiplied by 3 (345 x 3) to get 1035 with the 5 being placed directly under the number it is multiplied by which is 3. When we add all of these three results, we get 34500 + 6900 + 1035 = 42435.

Division

Divide 4560 by 5.

Procedure: In the above example, the 5 is the divisor, the 4560 is the dividend and the answer will be the quotient. Since 4 is not divisible by 5, zero (0) is placed above 4. We then go on to the number next to 4 which is 5 and so we then divide 45 by 5 to get 9. We then multiply the 9 by 5 to get 45. Now we then subtract 45 from the 45 above to get 0. We then bring down the number next to the 5 which is 6. We divide 6 by 5 to get 1. So we place the 1 above the 6 to get an interim result of 091. We then multiply the 1 by 5 to get 5 which we place under the 6; when this 5 is subtracted from 6 we get 1. Because we cannot divide 1 by 5, we bring down the 0 which makes it 10. When we divide 10 by 5, we get 2 which we place in the answer above to get 912 0r 912 because the 0 has no value. Because we cannot go any further, the answer is 912 which is the quotient.

Combining numbers together

The following example combines the use of addition, subtract, multiplication and division.

Example

Following the BODMAS acronym, we obtain:

(18 – 9) + 14 ÷ 7 x 3 so:

We have

18 – 9 = 9 because we must do the B or bracket first and so:

9 + 14 ÷ 7 x 3

Because D for division comes next, 9 + 2 x 3. Then, because M for multiplication comes next, we have, 9 + 6 and because A for addition comes next, we have: 9 + 6 = 15.

Decimals can consist of a whole number and a decimal fraction such as:

Decimal = Whole number + Decimal fraction

10.6 = 10 + 0.6

Decimal fractions are numbers that are written after decimal points such as: 0.6 = 6/10 as in the above case. The numbers after the decimal point are like the numerators of a fraction, with the denominator being 1 plus the amount of zeros equal to or corresponding to the amount of digits after the decimal point. Therefore, 0.25 = 25/100 or 0.025 = 25/1000.

Addition

When adding and subtracting decimal terms, we must line-up the points then insert 0s when necessary.

Simplify:

49.07 + 27.123 + 5.7223

"$ \bbox[5px,border:2px solid black] { \begin{align} & \\ &&49.0700 && \\  &+ &27.1230 && \\ &&5.7223 && \\ &&\overline{81.9153} && \\ & \end{align} } $"

Subtraction

Simplify:

48.3 – 8.23

"$ \bbox[5px,border:2px solid black] { \begin{align} & \\ &&48.30 && \\  &- &8.23 && \\  &&\overline{40.07} && \\ & \end{align} } $"

Multiplication

The procedure for multiplying decimals is the same as multiplying whole numbers. However, after completing the multiplication, the next step is to determine where the decimal point should be placed in the answer. This can be determined by counting the amount of decimal places in both the Multiplicand (number to be multiplied) and the Multiplier and then adjust the multiplied answer or product (from right to left) according to the amount of decimal places. Therefore, multiply the 44.2 by 12.9 below and the answer will be 57018. There is one decimal place in 44.2 and another in 12.9 resulting in two decimal places. So adjust the 57018 to two decimal places from right to left and the final answer will be 570.18.

Example

Simplify:

44.2 x 12.9

Division

The situation for dividing decimals is different from that of multiplying. Before dividing, turn the divisor (the number that is doing the dividing) into a whole number by moving the decimal point to the right after the last digit. After doing the foregoing, also move the decimal point of the number being divided (the dividend) to the right by the same amount of places as the divisor was moved. After this is done, do the division to produce the result or the quotient.

Example

Simplify:

48 ÷ 0.002

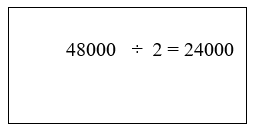
The 2 as the divisor was obtained by converting the 0.002 into a whole number which is done by shifting the decimal point 3 places to the right and doing the same thing to the 48 thereby converting it to 48000. The answer or quotient is 24000.

Decimal Places

To approximate a number to a given amount of decimal places follow the instructions outlined in the example below.

Example

Estimate 1979.5687 correct to 2 decimal places.

Solution

Count from left to right 2 decimal after the decimal point. We will get 1979.56 and if the next number to the right of this 56 is 5 or more (in this case it is 8), we add a 1 to the 6 making the answer 1979.57.

Example

Estimate 1979.5687 correct to 3 decimal places.

Solution

Count from left to right 3 places after the decimal point. We will get 1979.568 and if the next number to the right of this 568 is 5 or more (in this case it is 7), we add a 1 to the 8 making the answer 1979.569.

Significant Figures

When we are faced with a long number, we could round it off to the nearest thousand, or nearest million. Also, when we get a long decimal answer, we could round it off to a certain number of decimal places. Another method of giving an approximated answer is to round off using significant figures. The word significant means: having meaning. With the number 568249, the 5 is the most significant digit, because it tells us that the number is 5 hundred thousand and something. With the number 0.0000098763, the 9 is the most significant digit, because it tells us that the number is 9 millionths and something. The 8 is the next most significant, and so on.

In order to approximate a number to a given amount of significant figures (sf), see the following:

Example

208.70423

Estimate the above number to:

1. 6 sf
2. 5 sf
3. 4 sf
4. 3 sf
5. 2 sf
6. 1 sf

Solution:

1. To 6 sf = 208.70423 or 208.704

   Count from the left to the right, the number of sf and the answer is 208. 704523 which is the highlighted digits.

2. To 5 sf = 208.704523 or 208.70

3. To 4 sf = 208.704523 or 208.7

4. To 3 sf = 208.704523 or 209

   Counting from left to right, the 3^rd number is 8 but the next number after 8 is greater than 5 and so we have to add a 1 to the 8 making it 209.

5. To 2 sf = 208. 704523 or 210

   Again counting from left to right, the 2^nd number is 0 but the next number to the right (9) is 5 or more so we have to add 1 to the 0 making the answer 21. We must add a 0 to the 21 because we need 3 numbers before the decimal point. So the answer is 210.

6. To 1 sf = 209. 704523 or 200

   Again counting from the left, the 1^st number is 2 but the next number to the right is 0 which is less than 5 so we do not have to add 1 to the 0 making the answer 200. We must add 2 zeros to the 2 because we need 3 numbers before the decimal point. So the answer is 200.

Example

Write 0.0005678 to 1 significant figure (sf)

Solution

Counting from the left to right, the very first number is 5 and since the very next number which is 6 is more than 5, we add a 1 to the 5 making the answer 0.0006.

Standard Form and Scientific Notation

Standard form is another name for scientific notation. In standard form, the numbers are written in the form:

A x 10ⁿ

Where, 1 ≤ A ≤ 10, are in Standard Form.

Scientific notation is used to represent very large and very small numbers. In scientific notation, a number is written as a number between 1 and 10 multiplied by a power of 10. When writing a number in standard form, write the number in the form A. That is, turn the number into a number greater than or equal to 1 and or less than 10. This is done by moving the decimal point either to the right or to the left. The decimal point must be placed 1 point after the first number and then multiply by 10 raised to the negative or positive power equal to the number of decimal places or points that were to the required to move it to the decimal place after the first significant number. We then write the number in the form A x 10ⁿ.

Procedure for large numbers:

Step 1: Move the decimal point to the left until you have a number greater than or equal to 1 and less than 10.

Step 2: Count the number of decimal places you moved the decimal point to the left and use that number as the positive power of 10.

Step 3: Multiply the decimal (in Step 1) by the power of 10 (in Step 2).

Procedure for small numbers:

Step 1: Move the decimal point to the right until you have a number greater than or equal to 1 and less than 10.

Step 2: Count the number of decimal places you moved the decimal point to the right and use that number as the negative power of 10.

Step 3: Multiply the decimal (in Step 1) by the power of 10 (in Step 2).

Examples

Write the following numbers in standard form:

1. 926876
2. 0.000461234

Solution

1. 9.26876 x 10⁵
2. 4.61234 x 10^-4

Percentage or Fraction of a Quantity

To find the percentage of a quantity, express the percentage as a fraction (write the percentage given over 100) and multiply by the quantity.

Example

What is 50% of 400?

50/100 x 400 = 200

To find the fraction of a given quantity, multiply the fraction by the quantity.

Example

4/5 of 200

4/5 x 200 = 160

A Quantity as a Percentage or Fraction of Another

To express a quantity as a percentage of another quantity, divide the first quantity by the second and multiply by 100.

Example

Express 40 as a percentage of 800

40/800 x 100 = 5

Ratio

A ratio is a comparison between similar quantities. A ratio can be expressed as a fraction.

Example

A man shared $300 between Joe and Frank in the ratio of 2 : 1. How much money did both boys get? Just add the 2 and the 1 which is 3 which forms the denominator. Then place the proportions (the 2:1) over the denominator to give: 2/ 3 and 1/ 2 then multiply these by the 200.

Joe = 2/3 x 300 = $200

Frank = 1/3 x 300 = $100.

Squares, Square Root and Surds

Squares

To square a number, just multiply it by itself:

Example

4² = 4 times 4 = 16

15² = 15 times 15 = 225

When squaring negative numbers, the result will always be a positive as a negative number (-) times a negative number (-1) will result in or give a positive result.

Example

(-8)² = (-8) times (-8) = 64.

Square Root

A square root goes the other way. A square root of a number will give a number that when multiplied by itself, will produce the original or initial number. For example, the square root of 16 is 4 and when 4 is multiplied by itself, it will give the original number which is 16. The following is the square root sign:

"$\sqrt{  }$"

Example

"$\sqrt{16} = 4$"

So 

Example

"$ \begin{align} \sqrt{\frac{9}{4}} = \frac{3}{2} \end{align} $"

We cannot find the square root of a negative number.

Surds

Surds are numbers that cannot produce a square root directly. Some sort of manipulation is required to transform this expression in order for part of it to ne square rooted.

Rule #1:

"$ \sqrt{3 \times 3} = \sqrt{3} \times \sqrt{3} $"

Example

"$ \sqrt{27} = \sqrt{9} \times \sqrt{3} = 3 \sqrt{3} $"

Rule #2:

"$ \begin{align} \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}} \end{align} $"

Rule #3:

"$ \begin{align} \frac{x}{\sqrt{y}} = \frac{x}{\sqrt{y}} \times \frac{\sqrt{y}}{\sqrt{y}} = \frac{x \sqrt{y}}{y} \end{align} $"

Example

"$ \begin{align} \frac{5}{\sqrt{8}} = \frac{5}{\sqrt{8}} \times \frac{\sqrt{8}}{\sqrt{8}} = \frac{5 \sqrt{8}}{8} \end{align} $"

Rule #4

"$ = x \sqrt{w} \pm y \sqrt{w} = \left(x \pm y \right) \sqrt{w} $"

Example

"$ = 3 \sqrt{5} \pm 4 \sqrt{5} = \left(3 \pm 4 \right) \sqrt{5} $"

Rule #5

"$ \begin{align} \frac{w}{x + y \sqrt{z}} \end{align} $"

then multiply the numerator and denominator by "$ x - y \sqrt{z} $" 

Example

Rationalise the following:

"$ \begin{align} \frac{- 5}{2 + \sqrt{2}} &= \frac{5}{2 + \sqrt{2}} \times \frac{2 - \sqrt{2}}{2 - \sqrt{2}} = \frac{10 - 5 \sqrt{2}}{4 - 2} \\ & \\ & = \frac{10 - 5 \sqrt{2}}{2} \end{align} $"

Next - Number Theory