Previous - Algebra 2: Solving for Equations
Types and Properties of Angles
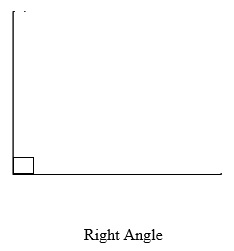
Right Angles
Angles which measure exactly 90° are right angles, that is, ϴ = 90°.
Acute Angles
Acute angles are angles which are greater than 0° but less than 90°, that is, 0° < ϴ < 90°.

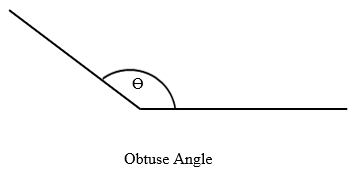
Obtuse Angles
Obtuse angles are those which are greater than 90° but less than 180°, that is, 90° < ϴ < 180°.
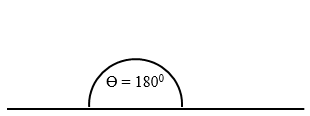
Straight Angles
Angles which measure exactly 180° (degrees) are straight angles. Therefore, straight angles are straight lines. Angles are represented by the sign ϴ, called theta. That is, for straight angles, ϴ= 180°.
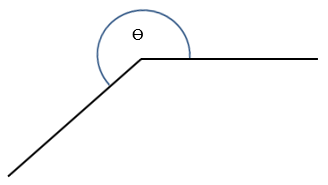
Reflex Angles
Reflex angles are angles which are greater than 180° but less than 360°, that is, 180° < ϴ < 360°.
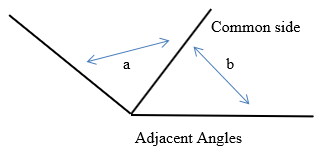
Adjacent Angles
Two angles which share the same vertex and have a common side (line) are called adjacent angles.
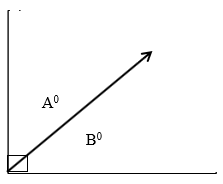
Complementary Angles
Complementary angles are two angles which when summed equal 90°.
A° + B° = 90°
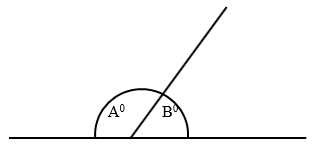
Supplementary Angles
Supplementary angles are two angles which when summed equals 180° such as:
A° + B° = 180°
Vertically Opposite Angles
Vertically opposite angles are the angles opposite to each other when two straight lines intersect. Their defining property is that, vertically opposite angles are equal in magnitude. For example, A=B and C=D.

Corresponding Angles
When two parallel lines are crossed by a line, this line is called a transversal. The angles formed by this crossing of the parallel lines by the transversal are called corresponding angles and these angles are equal in magnitude.

Corresponding angles:
b = f
d = h
a = e
c = g
Types and Properties of Triangles
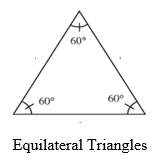
Equilateral Triangles
Equilateral triangles are those with all three sides equal in length and all three angles equal in size. Since the angles in a triangle sum to 180° and the size of each angle is the same in an equilateral triangle, the angles are all 60°.
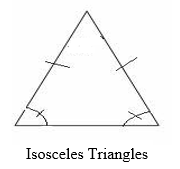
Isosceles Triangles
Isosceles triangles are triangles with two sides equal in length and two angles equal in size.
Scalene Triangles
A scalene triangle is one which has no sides equal in length and no angles equal in magnitude.
Congruent Triangles
Congruent triangles are triangles which have the same area, angles and side lengths.
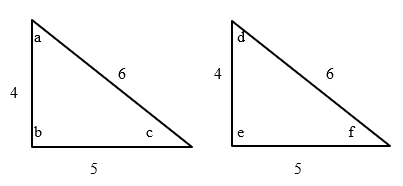
| Angles | Sides |
| a=d | 6=6 |
| b=e | 4=4 |
| c=f | 5=5 |
Similar Triangles
Triangles are similar if they have the same shape, but not necessarily the same size. Two triangles are similar if the only difference is size and possibly the need to turn or flip one round.
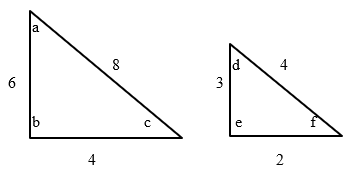
| Angles | Sides |
| a=d | 8≠4 |
| b=e | 6≠3 |
| c=f | 4≠2 |
Note: With similar angles, the angles are equal but not the sides.