Previous - Geometry 2: Trigonometry

Distance

Measuring distance in the coordinate plane can be done using Pythagorean theorem. If two points are given (x₁, y₁) and (x₂ y₂), their distance will always be given by the following formula:

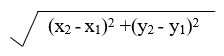
The distance between two points can be represented by the hypotenuse of a right triangle whose legs are of lengths (x₂, x₁) and (y₂, y₁). The following diagram shows how the formula is based on the Pythagorean theorem.

Example

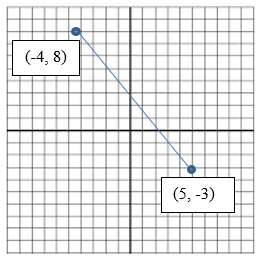
Calculate the distance between (5,–3) and (–4,8).  The solution of this problem requires that we substitute theses x and y values into the equation.

Solution

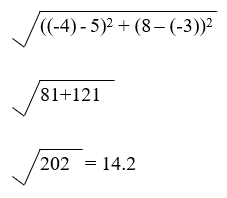
Therefore, the distance between (5,–3) and (–4, 8) is 14.2.

Finding Midpoints

Like finding the distance between two points, the midpoint between two points in the coordinate plane can be calculated using a formula. If the endpoints of a line segment are (x₁, y₁) and (x₂, ₂) then the midpoint of the line segment is:

Midpoint = (x1 + x2,  y1 + y2)
                             2                 2

In other words, the x- and y-coordinates of the midpoint are the averages of the x- and y-coordinates of the endpoints.

Example

What is the midpoint of the line segment whose endpoints are (6, 2) and (2, 8)?

Solution

Midpoint = (6 + 2),    (2 + 8)
                         2              2

                =  8  , 10   
                    2     2

So the midpoint is (4, 5).

Slope

The slope of a line is a measurement of how steeply the line climbs or falls as it moves from left to right. Therefore, the slope is a line’s vertical change divided by its horizontal change, also known as “rise over run.”

Given two points on a line, (x₁, y₁) and (x₂, y₂), the slope of the line can be calculated using the following formula:

Slope m = y2 - y1
                             x2 - x1

Example

Find the slope of a line that contains the points (–2,–3) and (6, 2) is:

Solution

m = y2 - y1
        x2 - x1

    = 2 – (-3)   = 5/8
       6 – (-2)     

m = 5/8

Equation of a Circle

The equation of a circle takes two forms which are:

1) The standard form:  (x - h)²  +  (y-k)²   =   r²

2) The general form  :  x²  +  y²  +  Dx  +  Ey  +  F   =   0,   where D, E, F are constants.

It must be noted that radius is always positive.

If the equation of a circle is in the standard form, we can easily identify the center of the circle, (h, k), and the radius, r .  

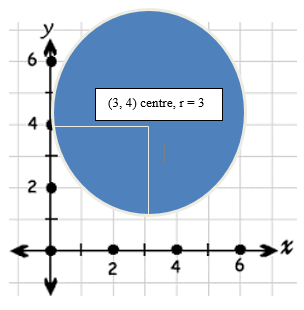
Example 1:   Given (x-3)² + (y-4)² = 9².   (a)  Find the center and radius of the circle.  (b) Graph the circle. 

Solution

Note:    A common mistake is to take h= -3 and k= -4.   In an equation, if the sign preceding h and k , ( h, k)  are  negative, then h and k are positive.  That is, h= 3 and k= 4.

(a)  Center: (h= 3, k= 4) = (3, 4)    and radius   r=3   since    r² =  9.   

Example 2

Find the centre and radius of the circle having the equation:

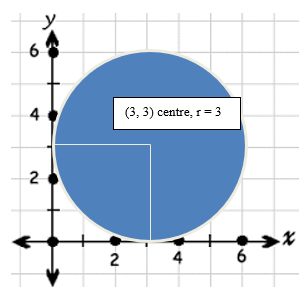
x² + y² – 6x – 6y + 9= 0.

Solution

If the equation is in the general form, we have to complete the square and bring the equation in the standard form.  Then, we can identify the center and radius correctly.  

First move the constant to the right side of the equation by subtracting it to get:

x² + y² –6x – 6y = -9

Then group the like terms to get:

x² – 6x + y²– 6y = -9

(x² – 6x + ….. + (y²– 6y + …..) = -9

Then take the x-term coefficient (which is 6), multiply it by one-half, square it, and then add this to both sides of the equation as shown below. Do the same with the y-term coefficient (which is also 6) and add to both sides of the equation. 

(x² – 6x + 9 )  + (y² – 6y + 9) = -9 + 9 + 9.

= (x² – 6x + 9 )  + (y² – 6y + 9) = 9.

Convert the left side to squared form, and simplify the right side.

(x – 3)² + (y – 3)²

The center is at (h, k) = (x, y) = (3, 3).

The radius is r = square root of 9 = 3.

Next - Statistics