Previous - Measurement 2: Surface Area and Volume

Algebraic Expressions

Algebraic expressions are expressions which contain terms, variables and coefficients, and constants.  The following is an example of an algebraic expression:

"$ x^2 + 6x + 9 $"

Terms

Terms are the elements in an algebraic expression separated by the arithmetic signs such as:

The terms in the expression:

"$ x^2 + 6x + 9 $"
"$ x^2 $"
"$ 6x $"
"$ 9 $"

A term may consist of variables and coefficients, or a constant.

Variables

The letters in a term are called variables. In the following expression:

"$ 3x + 4y - 5z $", the variables are: x, y and z.

Coefficients

Coefficients are the numbers before variables.

Example

In the following expression,

"$ 4x^2 + 6x + 9 $", the coefficients are:

"$4$" and "$6$"

Constants

Constants are the terms that contain numbers only.

Example  

In the following expression,

"$ 4x^2 + 6x + 9 $", the constant is 9.

Conducting Operations on Algebraic Expressions

Addition and Subtraction

The rules for the addition and subtraction of algebraic expressions are as follows:

Step 1: Group like terms because only like terms can be added and subtracted.

Step 2: Add or subtract the coefficients of the grouped like terms.

Example

1. "$ 4x + 3x + 2x – x $"

   "$ 9x – x = 8x $"

2. "$ 7x^2 + 6x – 8x – 3x^2 $"

   "$ 4x^2 – 2x $"

3. "$ 7x^3 + 5x^2 + 9x – 8x – 3x^2 $"

   "$ 7x^3 + 2x^2 + x $"

Multiplication and Division

The rules for the multiplication and division of positive and negative numbers are as follows:

Rules for multiplication:

Step 1: State the coefficients and variables of each term separately.

Step 2: Multiply the coefficients, constants and variables.

Note when multiplying variables:

"$ x^5 = x \times x \times x \times x \times x $"

Rules for division:

Step 1: State the coefficients and variables of each term separately.

Step 2: Divide the coefficients, variables and constants by the coefficients, variables and  constants in the denominator.

Step 3: Cancel the like variables in the numerator by those in the denominator.

Examples

"$ \frac{x^8}{x^6} = x^{8-6 =2} = x^2 $"

"$ \frac{8x^8}{2x^6} = 4x^{8-6 =2} = 4x^2 $"

Substituting Numbers for Algebraic Symbols

The values of algebraic expressions are obtained by substituting numbers in place of variables, and simplifying.

Example

Given "$ x=2 $" and "$ y=3 $",

Calculate:

"$ 4x^2 + 6x + 9 $",

Solution

"$ 4 \left( 2 \right) ^2 – 6 \left( 3 \right) + 9 = 16 – 18 + 9 = 7 $".

Removing and Inserting Brackets

Removing Brackets

The distributive law is used when removing brackets. It is summarised by the identity below:

"$ c \left( a + b \right) = c \times a + c \times b $"

The distributive law basically states that when removing a bracket, use the term outside the bracket to multiply each term in the bracket.

Examples

"$ 4 \left( 4x + 2 \right) = 16x + 8 $"

"$ 4 \left( 4x + 3x \right) = 16x^2 + 12x $"

"$ 5x \left( 2x^2 – x + 2 \right) = 10x^3 – 5x^2 + 10x $"

"$ -2x \left( x + 1 \right) = -2x^2 - 2 $"

Inserting Brackets or Factorising

The distributive law is also used to insert brackets. However, when inserting brackets, the law is used in reverse.

The distributive law in reverse is a means of factorizing. Factorization is the breakdown of numbers into factors, which when multiplied, yields the original numbers.

Rules for factorizing are as follows:

Step 1: Write the variables and coefficients/factor common to all the terms outside the brackets.

Step 2:  Divide each term inside the bracket by the term placed outside the brackets in step 1, placing the quotient of the divisions inside the brackets while leaving the common coefficient/common factor outside the bracket.

Examples

"$ 4x + 2 = 2 \left(2x + 1 \right) $"

"$ 4x^2 – 8x = 4x \left(x – 2 \right) $"

Multiplying algebraic expressions

In multiplying algebraic expressions, we can apply the distributive rule.

Example:

Multiply "$ 2x \left( 3xy + 7xy \right) $"

Solution:

"$ 6 x^2 y + 14x^2 y $"

Example:

Multiply "$ \frac{-3}{5x} \left( 15xy – 4 \right) $"

Solution:

"$ \left(- 3/ 5x \text{ times } 15xy \right) + \left(-3/ 5 \text{ times } – 4 \right) $"

"$ = -9xy + 12/ 5x $"

Multiplying monomials and polynomials

Example: Multiply (x + 2y) (3x − 2y + 5)

Solution

"$ \left( x + 2y \right) \left( 3x − 2y + 5 \right) = $"

"$ 3x^2 − 2xy + 5x + 6yx − 4y^2 + 10y = $"

"$ 3x^2 + 4xy + 5x − 4y^2 + 10y $"

Note: "$−2xy$" and "$6xy$" are added because they are Like Terms and also "$6yx$" means the same thing as "$6xy$".

Dividing a Polynomial

Dividing a polynomial by something more complicated than just a simple monomial requires the use of a method called long polynomial division and it works just like the long numerical division.

Example

Divide "$ x^2 – 8x – 9 $" by "$ x + 1 $"

Step 1:

Set up the division, putting the dividend (the thing being divided into) inside and the divisor (the thing doing the dividing) outside and to the left:

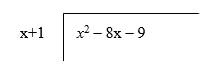
Step 2:

Divide the leading x² of the dividend by the leading x in front to get an x on top of the division symbol, right above the x² inside:

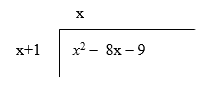
Step 3:

We then multiply the x through the divisor, x + 1.  We first multiply the x (on top) by the x (on the side) to get x², and carry the resulting x² underneath, putting it directly below the x² from the dividend.

Step 4:

Next we multiply the x on top by the 1 on the side to get 1x and we then place the 1x underneath placing it directly below the –8x in the dividend:

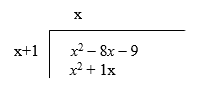
Step 5:

We now draw the horizontal "equals" bar underneath the dividend, so that the subtraction can be done.

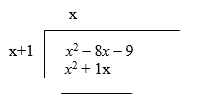
Step 6:

We must then subtract the top line by the bottom line which is the same as saying to change all the signs in the second line to get:

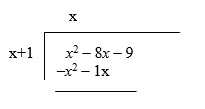
The next thing is to add where the first term (the x²) will cancel out because they have the same coefficient but opposite signs while the –8x – 1x becomes –9x:

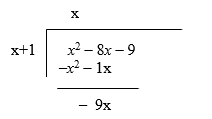
Step 7:

Like the normal long division, we now bring down the next figure in the dividend which is -9 to get:

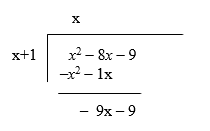
At this point, we start ignoring the dividend, and instead work on the bottom line of the long division.

We now look at the x from the divisor and the new leading term, the –9x, in the bottom line of the division. In dividing the –9x by the x, we will get –9 which must be placed on top, right above the –8x:

Step 8:

We now multiply the  – 9 on top by the leading x on the side, to get –9x which we will carry to the bottom, directly underneath the previous line's –9x to get:

Step 9:

We then multiply the –9 on top by the 1 on the side to get -9, and carry this –9 to the bottom, directly below the previous line's –9  to get:

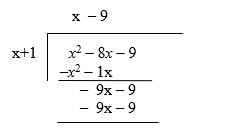
Step 10:

We will now draw another horizontal line and change the signs at the bottom line to get:

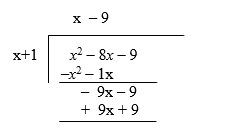
Adding both lines we get:

Because we ended with zeros, the division is complete and the answer is x - 9

To verify the answer, we can multiply x – 9 by x + 1 and see if we will get

x² – 8x – 9

So (x – 9) times (x + 1).

Step 1: x times x yields: x²  

Step 2: -9 times x and 1 times x yields: -9x + x = -8x.

Step 3: we are left with -9 times 1 which yields -9.

When combining these three terms, we get x² – 8x – 9, therefore,     

x² – 8x – 9 divided by x+1  is in fact equal to x  – 9.

Simplification of Algebraic Equations

Example:  Reduce the algebraic fraction 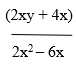 to its lowest term

Solution:

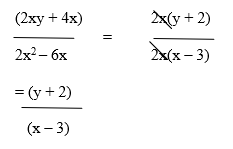
Example: Reduce the algebraic fraction 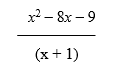 to its lowest terms.

Solution:

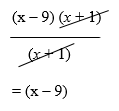
Example: Simplify 

Solution

Step 1: Find the lowest common factor (the Lowest Common Multiple of 6 and 3 is 6)

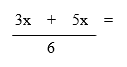
Step 2: Express denominator in the Lowest Common Multiple Form

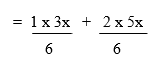
Step 3: Simplify the numerator

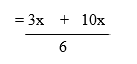
Step 4: Add the numerators to get:

Example

Simplify 

Solution

Step 1: Find the lowest common factor (the Lowest Common Multiple of 12 and 4 is 12)

Step 2: Express denominator in the Lowest Common Multiple Form

Step 3: Simplify the numerator

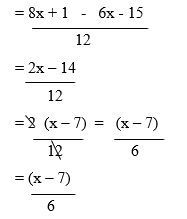
Note:

• Be careful of a minus sign before a bracket.
• Always reduce the final answer to its lowest terms.

Indices

A power, or an index, is used to write a product of numbers very compactly.  To manipulate math expressions, the law of indices must be considered. These laws can only apply to expressions with the same base such as 5⁴ and 5² which equals 5⁶ (restate the common base and just add the indices or powers).  It must be noted that the law of indices cannot be used in cases where the bases (5 and 4) are different such as 5⁴ and 4⁷.

The following are the rules for the Law of Indices:

Rule 1: a⁰ = 1

Rule 2: a^x  x a^y  = a^x+y

Rule 3: a^x  ÷  a^y  = a^x-y

Rule 4: a^-x = 1/a^x

Rule 5: a^x/y = ^y√a^x  or (^y√a)^x 

Rule 6: (a^x)^y = a^xy  

The laws of indices:

Examples

y⁰ = 1

3⁰ = 1

100⁰ = 1

Examples

2⁴ × 2⁸ = 2¹²

5⁴ × 5^-2 = 5^{2 (4-2)} 

(yⁿ)^m = y^nm

Examples

3⁹ ÷ 3⁴ = 3⁵

7² ÷ 7⁵ = 7^-3

y ^-b = 1/y^b

Examples

2^-3 = 1/2³ = 1/8

3^-1 = 1/3

y^m/n = (ⁿ√y)^m

Examples

16^1/2 = √16 = 4

8^2/3 = (³√8)² = 2² = 4

Example

2⁵ + 8⁴

= 2⁵ + (2³)⁴

= 2⁵ + 2¹²

Next - Algebra 2: Solving for Equations